Inoffizielle Probeprüfung DML WS-25

Disclaimer: “Diese Probeprüfung dient nur zu Übungszwecken. Sie deckt den ganzen Stoff nicht ab.”

180 min

90 Punkte je 10 pro Aufgabe

ca. 45 Punkte zum Bestehen

1. Induktion
2. Logik
3. Relationen
4. Äquivalenzrelationen
5. Ordnungsrelationen
6. Funktionen
7. Kombinatorik
8. Graphentheorie
9. Abzählen

Induktion 10 Pkt

Induktion I 5 Pkt

Zeigen Sie mittels vollständiger Induktion, dass für alle \(n ∈ ℕ\) gilt: \[ \sum_{k=1}^{n} k^3 = \left( \sum_{k=1}^{n} k \right)^2 \]

Hinweis: Benutzen Sie die Gaußsche Summenformel!

TipLösung

IA: \(n=0\)

\[ \sum_{k=1}^{0} k^3 = 0 = 0² = \left( \sum_{k=1}^{0} k \right)^2 \]

IS: \(n>0\)

\[ \begin{aligned} \sum_{k=1}^{n} k^3 &=_{(\text{IV})} \left( \sum_{k=1}^{n-1} k \right)^2 + n³\\ &=_{(\text{Gaußsche Summenformel})} \left( \frac{n(n-1)}{2} \right)^2 + n^3\\ &= \frac{n^2 - 2n^3 + n²}{4} + \frac{4n^3}{4}\\ &= \frac{n^2 + 2n^3 + n²}{4}\\ &= \left( \frac{n(n+1)}{2} \right)^2\\ &=_{(\text{Gaußsche Summenformel})} \left( \sum_{k=1}^{n} k \right)^2 \end{aligned} \]

Induktion II 5 Pkt

Zeigen Sie mittels vollständiger Induktion das Binomialtheorem:

Für alle \(n ∈ ℕ\) und \(0 ≤ k ≤ n\) gilt: \[ (a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k \] Hinweis: \(\binom{n-1}{k} + \binom{n-1}{k-1} = \binom{n}{k}\)

TipLösung

IA: \(n=0\)

\[ (a + b)^0 = 1 = \binom{0}{0} a^{0} b^0 = \sum_{k=0}^{n} \binom{0}{k} a^{0-k} b^k \]

IS: \(n>0\)

\[ \begin{aligned} (a + b)^n &= (a + b) \cdot (a + b)^{n-1} \\ &=_{(\text{IV})} (a + b) \cdot \sum_{k=0}^{n-1} \binom{n-1}{k} a^{(n-1)-k} b^k \\ &= \sum_{k=0}^{n-1} \binom{n-1}{k} a^{(n-1)-k+1} b^k + \sum_{k=0}^{n-1} \binom{n-1}{k} a^{(n-1)-k} b^{k+1} \\ &= \sum_{k=0}^{n-1} \binom{n-1}{k} a^{n-k} b^k + \sum_{k=1}^{n} \binom{n-1}{k-1} a^{n-k} b^k \\ &= \sum_{k=1}^{n-1} \left[ \binom{n-1}{k} + \binom{n-1}{k-1} \right] a^{n-k} b^k + \binom{n-1}{0}a^n b^0 + \binom{n-1}{n-1}a^0 b^n \\ &=_{(\text{Hinweis})} \sum_{k=1}^{n-1} \binom{n}{k} a^{n-k} b^k + \binom{n}{0} a^n b^0 + \binom{n}{n} a^0 b^n \\ &= \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k \end{aligned} \]

Logik 10 Pkt

Logische Äquivalenzen 5 Pkt

Zeigen Sie mittels logischer Äquivalenzen, dass: \(¬(A ⊕ B) ≡ ¬A ⊕ B ≡ A ⊕ ¬B\).

Geben Sie bei jedem Schritt an, welche logische Regel Sie angewendet haben. - Nutzen Sie: \(A ⊕ B ≡ (A ∧ ¬B) ∨ (¬A ∧ B) \quad (\text{Definition von } ⊕)\)

TipLösung

\[ \begin{aligned} ¬(A ⊕ B) &≡ ¬((A ∧ ¬B) ∨ (¬A ∧ B)) &(\text{Definition von } ⊕)\\ &≡ ¬(A ∧ ¬B) ∧ ¬(¬A ∧ B) &(\text{De Morgan})\\ &≡ (¬A ∨ B) ∧ (A ∨ ¬B) &(\text{De Morgan})\\ &≡ ((¬A ∨ B) ∧ A) ∨ ((¬A ∨ B) ∧ ¬B) &(\text{Distributivgesetz})\\ &≡ (¬A ∧ A) ∨ (¬A ∧ ¬B) ∨ (B ∧ A) ∨ (B ∧ ¬B) &(2\times\text{Distributivgesetz})\\ (*) &≡ (¬A ∧ ¬B) ∨ (A ∧ B) &(2\times\text{tertium non datur})\\ &≡ ¬A ⊕ B &(\text{Definition von } ⊕) \end{aligned} \]

und

\[ \begin{aligned} (*) &≡(¬A ∧ ¬B) ∨ (A ∧ B)\\ &≡ (A ∧ B) ∨ (¬A ∧ ¬B) &(\text{Kommutativgesetz})\\ &≡ A ⊕ ¬B &(\text{Definition von } ⊕) \end{aligned} \]

Wahrheitstabellen 5 Pkt

Betrachten sie folgende Julia-Funktion:

function f(x::Integer, y::Integer)::Bool
    if B(x ,y) && C(x, y)
        return A(x, y)
    else
        if B(x, y)
            return !A(x, y)
        else
            return A(x, y)
        end
    end
end

Wir können die Funktion auch als logische Formel schreiben:

\[f = \Big((B ∧ C) → A\Big) ∧ \Big(¬(B ∧ C) → \big((B → (¬A)) ∧ (¬B → A)\big)\Big)\]

Vereinfachen Sie die Formel mittels einer Wahrheitstabelle so weit wie möglich. Wie sieht die vereinfachte Funktion aus? - Schreiben sie die Funktion in Pseudocode/(Sprache ihrer Wahl).

TipLösung

Wahrheitstabelle erstellen:

\(A\)	\(B\)	\(C\)	\(\tiny B∧C=H_1\)	\(\tiny (B∧C)→A = H_3\)	\(\tiny B→¬A\)	\(\tiny ¬B→A\)	\(\tiny (B→¬A)∧(¬B→A)=H_2\)	\(\tiny H_4 = ¬H_1 \to H_2 \equiv H_1 \vee H_2\)	\(\tiny f = H_3 \wedge H_4\)
0	0	0	0	1	1	0	0	0	0
0	0	1	0	1	1	0	0	0	0
0	1	0	0	1	1	1	1	1	1
0	1	1	1	0	1	1	1	1	0
1	0	0	0	1	1	1	1	1	1
1	0	1	0	1	1	1	1	1	1
1	1	0	0	1	0	1	0	0	0
1	1	1	1	1	0	1	0	1	1

Vereinfachung:

\[ \begin{aligned} f ≡ (A ∧ ¬B) ∨ (B ∧ ¬A ∧ ¬C) ∨ (A ∧ B ∧ C) ≡ (A ∧ ¬B) ∨ (B ∧ (A ↔ C)) \end{aligned} \]

in Julia wäre das:

f(x,y) = (A(x,y) && !B(x,y)) || (B(x,y) && (A(x,y) == C(x,y)))

Relationen 10 Pkt

Betrachten sie die Funktion \(\text{Digits}\), die jeder natürlichen Zahl die Menge ihrer Ziffern zuordnet.

\(\text{Digits}: ℕ → \mathcal{P}(\{0,1,2,3,4,5,6,7,8,9\})\)

\(\text{Digits}(a) = \{ d ∈ \{0,1,2,3,4,5,6,7,8,9\} \mid (∃k ∈ ℕ) [d = ⌊\frac{a}{10^k}⌋ \mod 10]\}\)

Digits kann wie folgt berechnet werden:

function Digits(number::Integer)::Set{Integer}
    # Initialisiere die leere Menge
    set = Set{Integer}()
    # Sonderfall für 0
    if number == 0
        push!(set, 0)
        return set
    end
    while number > 0
        # Füge die letzte Ziffer von digits zu set hinzu
        push!(set, number % 10)
        # Entferne die letzte Ziffer von digits
        number ÷= 10
    end
    return set
end

z.B. \(\text{Digits}(1729) = \{1,2,7,9\}, \quad \text{Digits}(696) = \{6,9\}, \quad \text{Digits}(4002) = \{0, 2,4\}\).

Eigenschaften von Relationen 5 Pkt

Die Relation \(R_1 ⊆ ℕ × ℕ\) sei definiert durch:

\[ R_1 = \{(a,b) ∈ ℕ × ℕ \mid \text{Digits}(a) ⊆ \text{Digits}(b)\} \]

Finden Sie heraus, ob die Relation reflexiv, symmetrisch, antisymmetrisch, transitiv oder linear ist. Begründen Sie ihre Antworten.

1. reflexiv

TipLösung

Ja, denn für alle \(a ∈ ℕ\) gilt \(\text{Digits}(a) ⊆ \text{Digits}(a)\).

2. symmetrisch

TipLösung

Nein, denn: \((1,12) \in R_1\), aber \((12,1) ∉ R_1\), da \(\text{Digits}(1) = \{1\}\) und \(\text{Digits}(12) = \{1,2\}\) und somit \(\text{Digits}(12) ⊈ \text{Digits}(1)\).

3. antisymmetrisch

TipLösung

Nein, denn: \((21, 12) ∈ R_1\) und \((12, 21) ∈ R_1\)

4. transitiv

TipLösung

Ja, aus direkter Folge der Transitivität der Teilmengenrelation.

5. linear

TipLösung

Nein, denn: \((2,1) ∉ R_1\) und \((1,2) ∉ R_1\).

Äquivalenzen 3 Pkt

Betrachten Sie die Relation \(R_2 ⊆ ℕ × ℕ\):

\[R_2 = \{(a,b) ∈ ℕ × ℕ \mid \text{Digits}(a) = \text{Digits}(b)\} \]

Zeigen Sie, oder widerlegen Sie das \(R_2\) eine Äquivalenzrelation ist.

Falls \(R_2\) eine Äquivalenzrelation ist, wie viele Äquivalenzklassen gibt es?

Falls \(R_2\) keine Äquivalenzrelation ist, welche Elemente \(X\) müssten hinzugefügt werden, sodass \(R_2 ∪ X\) eine Äquivalenzrelation ist?

TipLösung

Wir zeigen, die drei Eigenschaften einer Äquivalenzrelation:

reflexiv: Für alle \(a ∈ ℕ\) gilt \(\text{Digits}(a) = \text{Digits}(a)\), also ist \((a,a) ∈ R_2\).

transitiv: Für alle \(a,b,c ∈ ℕ\) mit \((a,b) ∈ R_2\) und \((b,c) ∈ R_2\) gilt \(\text{Digits}(a) = \text{Digits}(b)\) und \(\text{Digits}(b) = \text{Digits}(c)\). Somit ist auch \(\text{Digits}(a) = \text{Digits}(c)\) und somit \((a,c) ∈ R_2\).

symmetrisch: Für alle \(a,b ∈ ℕ\) mit \((a,b) ∈ R_2\) gilt \(\text{Digits}(a) = \text{Digits}(b)\). Somit ist auch \(\text{Digits}(b) = \text{Digits}(a)\) und somit \((b,a) ∈ R_2\).

Damit ist \(R_2\) eine Äquivalenzrelation mit \(2^{10}\) Äquivalenzklassen.

Bedingungen von Halbordnungen 2 Pkt

Betrachten Sie die Relation \(R_3 ⊆ ℕ × ℕ\), die der Relation \(R_1\) ähnlich ist:

\[ R_3 = \{(a,b) ∈ ℕ × ℕ \mid \text{Digits}(a) ⊆ \text{Digits}(b) ∧ λ\} \]

mit der nicht näher definierten Bedingung \(λ\).

Definieren sie die Bedingung \(λ\) so, dass \(R_3\) zu einer nicht symmetrischen Halbordnung wird. Was sind dann die minimalen Elemente von \((ℕ,R_3)\)?

TipLösung

Definieren wir \(λ\) als \(a ≤ b\). Dann ist \(R_3\) reflexiv, antisymmetrisch und transitiv, aber nicht symmetrisch.

Dann sind die minimalen Elemente von \((ℕ,R_3)\) die einstelligen natürlichen Zahlen: \(\{0,1,2,3,4,5,6,7,8,9\}\).

Äquivalenzrelationen 10 Pkt

Folgender gerichteter Graph \(G = (A, R)\) veranschaulicht eine binäre Relation \(R\) auf der Grundmenge \(A = \{a, b, c, d, e, f \}\):

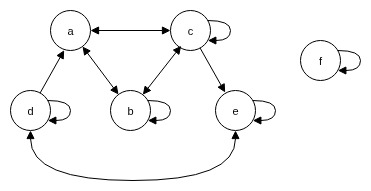
Äquivalenzrelationen I - 1.5 Pkt

Welche Kanten müssen dem Graphen hinzugefügt werden, damit \(R\) eine Äquivalenzrelation wird?

Geben Sie die Kanten an, sowie ein Repräsentantensystem der Äquivalenzklassen an.

TipLösung

Die Kanten, die hinzugefügt werden müssen, sind: \[\{(a,a), (a,d), (e,c), (d,c), (c,d), (d,b), (b,d), (b,e), (e,b), (e,a), (a,e) \}\]

Mit dem Repräsentantensystem der Äquivalenzklassen: \[\{a,f\}\]

Äquivalenzrelationen II - 1.5 Pkt

Welche Kante muss hinzugefügt und welche zwei Kanten müssen dem Graphen entfernt werden, damit \(R\) eine Äquivalenzrelation wird?

Geben Sie die Kanten an, sowie ein Repräsentantensystem der Äquivalenzklassen an.

TipLösung

Die Kanten, die hinzugefügt werden muss ist:\((a,a)\)

Die Kanten, die entfernt werden müssen sind: \((d,a), (c,e)\)

Mit dem Repräsentantensystem der Äquivalenzklassen: \[\{a,d,f\}\]

Modulo - 2 Pkt

Geben Sie die Menge der Äquivalenzklassen von \(M = \{ (x, y) ∣ (x^2 \mod 5) = (y^2 \mod 5) \} ⊆ ℕ²\) an.

TipLösung

Wir erinnern uns das für mod gilt: \[ (a \cdot b) \mod m = [(a \mod m) \cdot (b \mod m)] \mod m \]

Die möglichen Reste sind dann: \((1 \cdot 1) \mod 5 = 1\), \((2 \cdot 2) \mod 5 = 4\), \((3 \cdot 3) \mod 5 = 9 \mod 5 = 4\), \((4 \cdot 4) \mod 5 = 16 \mod 5 = 1\), \((0 \cdot 0) \mod 5 = 0\).

Somit ergeben sich die Äquivalenzklassen:

\(M_0 = \{x \in ℕ \mid x² \mod 5 = 0\} = \{0, 5, 10, 15, ...\}\)

\(M_1 = \{x \in ℕ \mid x² \mod 5 = 1\} = \{1, 4, 6, 9, 11, 14, ...\}\)

\(M_4 = \{x \in ℕ \mid x² \mod 5 = 4\} = \{2, 3, 7, 8, 12, 13, ...\}\)

Multidimensionale Representantensysteme - 1.5 Pkt

Sei \(W \subseteq ℝ^4 \times ℝ^4\) eine Äquivalenzrelation wobei \([-\frac{π}{2}, \frac{π}{2}] \times ℝ_{≥0} \times \{0\} \times \{0\}\), \(\; [-\frac{π}{2}, \frac{π}{2}] \times \{0\} \times ℝ_{≥0} \times \{0\}\) und \(\; [-\frac{π}{2}, \frac{π}{2}] \times \{0\} \times \{0\} \times ℝ_{≥0}\) verschiedene Representatensysteme von \(W\) sind. Geben Sie ein passendes \(W\) an. - Hinweis: Sie benötigen die Sinusfunktion für die Definition von \(W\).

TipLösung

Sei \(W\) definiert als: \[W = \{((t_1, x_1, y_1, z_1), (t_2, x_2, y_2, z_2)) ∈ ℝ^4 × ℝ^4 \mid \sin(t_1) = \sin(t_2) ∧ x_1² + y_1² + z_1² = x_2² + y_2² + z_2²\}\]

Die Super Relation - 0.5 Pkt

Sei \(B\) eine Beliebige Menge. Welche Relation \(R ⊆ B × B\) ist sowohl Äquivalenzrelation, Halbordnung und zugleich eine Bijektion?

TipLösung

Die Identitätsrelation: \[R = \{(a,a) ∣ a ∈ B\}\]

Kombinatorik der Äquivalenzrelationen - 3 Pkt

1. Wie viele verschiedene Äquivalenzrelationen gibt es auf der Menge \([4] = \{1,2,3,4\}\) - 1 Pkt

TipLösung

Das entspricht der sogenannten Bell-Zahl \(B_4\): \[ B_4 = \sum_{i = 1}^{4} \left\{ { 4 \atop i} \right\} = 1 + 7 + 6 + 1 = 15 \]

2. Wie viele Möglichkeiten gibt es, die Menge \([n]\) in genau \(k\) intern geordnete Äquivalenzklassen zu partitionieren? Die Klassen selbst sind dabei geornet, aber zwischen jeweils zwei verschiedenen Klassen herscht keine Ordnung. - Hinweis: Sie benötigen für das Lösen dieser Aufgabe keine Stirling-Zahlen - 2 Pkt

TipLösung

Wir ordnen zuerst die \(n\) Elemente in einer Reihenfolge an. Das sind \(n!\) Möglichkeiten.

Dann wählen wir \(k-1\) Trenner aus den \(n-1\) Zwischenräumen der \(n\) Elemente aus. Das sind \(\binom{n-1}{k-1}\) Möglichkeiten.

Jetzt teilen wir die Anordnung an den Trennern in \(k\) intern geordnete Äquivalenzklassen auf. \(/k!\)

Dann erhalten wir: \[ \frac{n!}{k!} \binom{n-1}{k-1} \]

Ordnungsrelationen 10 Pkt

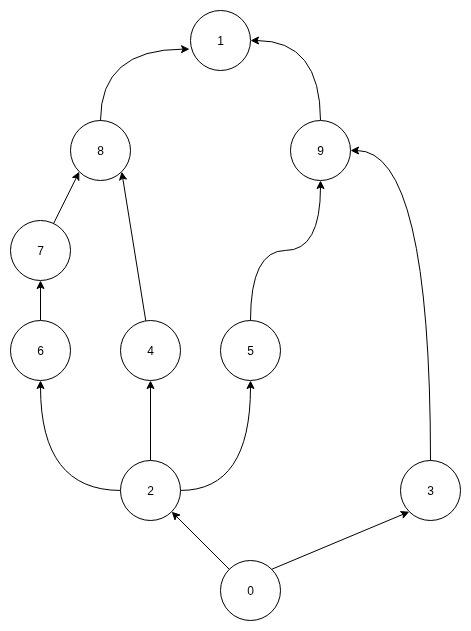
Betrachten Sie die Halbordnung \(⪯_H \; ⊆ [9] × [9]\) definiert durch folgendes Hasse-Diagramm:

Untere Schranken 2 Pkt

Sei nun \(O_1 = (\{9,8\}, ⪯_H)\) eine halbgeordnete Menge.

1. Was sind die unteren Schranken von \(O_1\)?

TipLösung

Untere Schranken von \(O_1\) sind: \(\{0,2\}\)

2. Was ist das Infimum von \(O_1\)?

TipLösung

das Infimum von \(O_1\) ist \(2\)

Obere Schranken 2 Pkt

Sei nun \(O_2 = (\{2,3\}, ⪯_H)\) eine halbgeordnete Menge.

1. Was sind die oberen Schranken von \(O_2\)?

TipLösung

Oberen Schranken von \(O_2\) sind: \(\{1,9\}\)

2. Was ist das Supremum von \(O_2\)?

TipLösung

Das Supremum von \(O_2\) ist \(9\)

Die Quersumme einer Zahl bezüglich der Basis \(10\), \(q_{10}:ℕ → ℕ\), kann wie folgt berechnet werden:

function q₁₀(n::Integer)::Integer
    sum = 0
    while n > 0
        sum += n % 10 # sum = n mod 10
        n ÷= 10 # n = ⌊n / 10⌋
    end
    return sum
end

z.B \(q_{10}(1729) = 1 + 7 + 2 + 9 = 19, \quad q_{10}(13) = 1 + 3 = 4\)

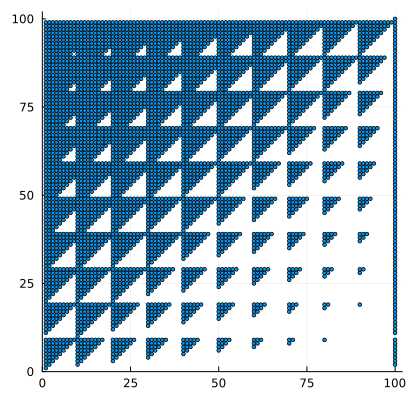
Die Halbordnung \(⪯_{q_{10}} ⊆ ℕ × ℕ\) ist definiert durch:

\[ ⪯_{q_{10}} = \{(a,b) ∈ ℕ × ℕ ∣ q_{10}(a) < q_{10}(b) ∨ a = b\} \]

\[\quad ⪯_{q_{10}} \text{angewendet auf} [100] × [100]\]

Hasse-Diagramm 2 Pkt

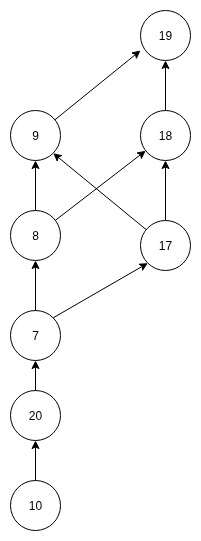
Zeichnen Sie das Hasse-Diagramm der halbgeordneten Menge \((\; \left( [7, 10] ∪ [17, 20] \right) ∩ ℕ \;,⪯_{q_{10}})\). - Hinweis: Das muss nicht schön sein, nur lesbar

TipLösung

Bedingungen der Ordnung 3 Pkt

1. Zeigen Sie, dass \(⪯_{q_{10}}\) eine Halbordnung ist. - 2 Pkt

TipLösung

Wir zeigen die drei Eigenschaften einer Halbordnung:

reflexiv: Für alle \(a ∈ ℕ\) gilt \(q_{10}(a) = q_{10}(a)\), also ist \((a,a) ∈ ⪯_{q_{10}}\).

transitiv: Für alle \(a,b,c ∈ ℕ\) mit \((a,b) ∈ ⪯_{q_{10}}\) und \((b,c) ∈ ⪯_{q_{10}}\) gilt entweder \(a = b\) oder \(q_{10}(a) < q_{10}(b)\) und entweder \(b = c\) oder \(q_{10}(b) < q_{10}(c)\). In allen Fällen folgt daraus, dass entweder \(a = c\) oder \(q_{10}(a) < q_{10}(c)\), also ist auch \((a,c) ∈ ⪯_{q_{10}}\).

antisymmetrisch: Für alle \(a,b ∈ ℕ\) mit \((a,b) ∈ ⪯_{q_{10}}\) und \((b,a) ∈ ⪯_{q_{10}}\) gilt entweder \(a = b\) oder \(q_{10}(a) < q_{10}(b)\) und entweder \(b = a\) oder \(q_{10}(b) < q_{10}(a)\). Die einzigen Möglichkeiten sind also \(a = b\).

2. Zeigen Sie, dass \(⪯_{q_{10}}\) keine Ordnung ist. - 1 Pkt

TipLösung

Gegenbeispiel: \(1 \not ⪯_{q_{10}} 100\) und \(100 \not ⪯_{q_{10}} 1\) und somit ist \(⪯_{q_{10}}\) nicht linear.

Minimale Elemente 1 Pkt

Was ist die Menge der minimalen Elemente bezüglich der halbgeordneten Menge \((ℕ_+,⪯_{q_{10}})\)?

TipLösung

\[ \{x \in ℕ_+ \mid (∃e \in ℕ) \big[ 10^e = x \big]\} = \{1, 10, 100, ...\} \]

Funktionen 10 Pkt

Eigenschaften von Funktionen 2 Pkt

Gegeben sind 4 Relationen \(R_i ⊆ [0,100] × [0, 100]\) für \(i ∈ [4]\):

Wobei die Horizontale Achse den ersten(linken) Wert des Tupels und die Vertikale Achse den zweiten(rechten) Wert des Tupels darstellt.

Kreuzen sie an, welche der Eigenschaften auf die Relationen zutreffen:

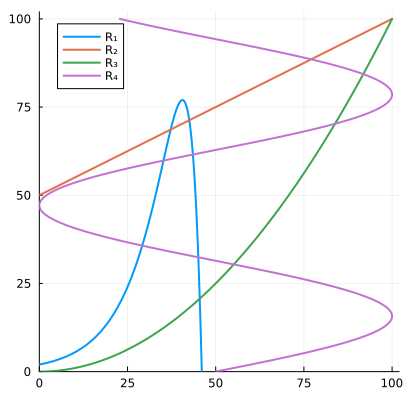
Relation	linkstotal	linkseindeutig	rechtstotal	rechtseindeutig
\(R_1\)	□	□	□	□
\(R_2\)	□	□	□	□
\(R_3\)	□	□	□	□
\(R_4\)	□	□	□	□

TipLösung

Relation	linkstotal	linkseindeutig	rechtstotal	rechtseindeutig
\(R_1\)	□	□	□	⊠
\(R_2\)	⊠	⊠	□	⊠
\(R_3\)	⊠	⊠	⊠	⊠
\(R_4\)	⊠	⊠	⊠	□

Sei \(f: ℕ × ℕ → ℕ\) eine Funktion definiert durch: \[ f(x,y) = x² + yˣ\]

Bildmenge 2 Pkt

Geben Sie die Bildmenge \(f(A)\) von \(A = \{ (x,y) ∈ ℕ × ℕ \mid 0 < x + y ≤ 2 \}\) unter \(f\) an.

TipLösung

\(A = \{(1,0), (0,1), (1,1), (0,2), (2,0)\}\)

\(f(A) = \{(1+0),(0+1),(1+1), (0+1), (4+0)\} = \{1,2,4\}\)

Urbildmenge 2 Pkt

Geben Sie die Urbildmenge \(f⁻¹(B)\) von \(B = \{ n ∈ ℕ \mid n < 5 ∧ (∃m ∈ ℕ)[m² = n] \}\) unter \(f\) an. - Hinweis: 0⁰ := 1

TipLösung

\(B = \{0, 1, 4\}\)

\(f^{-1}(0) = ∅\)

\(f^{-1}(1) = \{(0,1), (1,0), (0,0), (0,2)\}\)

\(f^{-1}(4) = \{(2,0), (1,3)\}\)

somit ist:

\[ f^{-1}(B) = \{(0,1), (1,0), (0.0), (0,2), (2,0), (1,3)\} \]

Injektionen und Surjektionen 2 Pkt

Seien A, B zwei endliche Mengen. Es existieren eine surjektive Funktion \(s: A → B\) die jedoch nicht injektiv ist. Welche der folgenden Aussagen gilt dann? Begründen Sie ihre Antwort.

1. Es existiert eine bijektive Funktion \(b: A → B\) mit einer inversen Funktion \(b⁻¹: B → A\).
2. Es existiert keine bijektive Funktion \(b: A → B\).
3. Es lässt sich noch nicht sagen, ob es eine bijektive Funktion \(b: A → B\) gibt oder nicht.

TipLösung

Die Aussage 2 ist korrekt. Denn da \(s\) nicht injektiv ist und \(A\) und \(B\) endlich sind, muss \(|A| > |B|\) gelten. Somit kann es keine bijektive Funktion von \(A\) nach \(B\) geben.

Hintereinanderausführung 2 Pkt

Gibt es eine injektive Funktion \(i: ℕ → ℕ\) die jedoch nicht surjektiv ist und eine surjektive Funktion \(s: ℕ → ℕ\) die jedoch nicht injektiv ist, sodass die Hintereinanderausführung von \(s ∘ i\) eine bijektive Funktion ist? – Wenn ja, welche? Wenn nein, warum nicht?

TipLösung

Ja, aber nur weil ℕ eine undendliche Menge ist, nähmlich:

\[ i(x) = 2x \]

und

\[ s(x) = \left\lfloor\frac{x}{2} \right\rfloor \]

dann ist:

\[ s ∘ i(x) = s(2x) = \left\lfloor\frac{2x}{2} \right\rfloor = x \]

Kombinatorik 10 Pkt

Ein Pokerdeck besteht aus 52 Karten \(F × W\), aufgeteilt in 4 Farben \(F = \{\text{Karo}, \text{Herz}, \text{Pik}, \text{Kreuz}\}\) mit jeweils 13 Werten \(W = \{2,3,4,5,6,7,8,9,10,\text{Bube},\text{Dame},\text{König},\text{Ass}\}\) der Grösse nach aufgelistet.

Beim 5-Card-Draw ziehen sie jeweils 5 Karten auf einmal in die Hand und können dabei verschiedene Kombinationen formen.

Karten in der Hand sind als Teilmenge von \(F × W\) zu betrachten bzw. die Hand ist nicht geordnet.

Hand 1 Pkt

1. Wie viele Möglichkeiten gibt es 5 Karten zu auf einmal ziehen? - Das Angeben der Formel genügt. - 0.5 Pkt

TipLösung

\[ \binom{52}{5} \]

2. Wie viele Möglichkeiten gäbe es 5 Karten nacheinander zu ziehen, wobei nun die Reihenfolge des Ziehens eine Ordnung \(≤_{\text{draw}}\) impliziert unter welcher wir unterscheiden? - 0.5 Pkt

TipLösung

\[ (52)_5 = \prod_{i=1}^{5} 52-i+1 \]

Im folgenden werden wir mit “ziehen” immer “5 Karten auf einmal ziehen” meinen.

Royal Flush 0.5 Pkt

Ein Royal Flush ist mit \(0.000154 %\) Auftrittswahrscheinlichkeit die seltenste und wertvollste Kombination. Dazu müssen sie in der Hand (10, Bube, Dame, König, Ass) von der selben Farbe haben.

Wie viele Möglichkeiten gibt es einen Royal Flush zu ziehen? - Bitte die vollständige Zahl angeben

TipLösung

Für jede Farbe gibt es nur eine Möglichkeit:

\[ 4 \]

Strasse 1 Pkt

Eine Strasse besteht aus 5 Karten mit 5 aufeinander folgenden Werten. Bsp: \((8,9,10,\text{Junge},\text{Dame})\)

Einfachhalt halber erlauben wir keine zyklischen Stassen wie \((\text{König}, \text{Ass}, 2, 3, 4)\) sondern nur welche die von klein nach gross gehen. Royal Flush und Staight Flush sind auch Stassen.

Wie viele Möglichkeiten gibt es eine Strasse zu ziehen. - Das angeben der Formel genügt.

TipLösung

Betrachten wir nur die Werte so fällt uns auf, das wir bei \(13\) Werten \(13 + 1 - 5\) verschidene Teilmengen mit aufeinander folgenden Werten bilden können.

Zu jedem der 5 Werte können wir dann jeweils eine von vier farben auswählen, also \(4^5\).

Zusammengesetzt erhalten wir:

\[ 9 \cdot 4^5 \]

Full House 2.5 Pkt

Ein Fullhouse besteht aus einem Drilling aus 3 gleichen Werten und einem Paar aus 2 gleichen Werten.

1. Wie viele Möglichkeiten haben sie ein Fullhouse zuerst zu ziehen, und dann in einer Reihe anzuordnen? - Das Angeben der Formel genügt. - 1 Pkt

TipLösung

Wir ziehen einen Drilling(\(\binom{13}{1}\)) und einen Zwilling(\(\binom{12}{1}\)). Die Reihenfolge ist dabei egal.

Für den Drilling wählen wir 3 Farben aus 4 (\(\binom{4}{3}\)) und für den Zwilling 2 Farben aus 4 (\(\binom{4}{2}\)).

Nun ordnen wir die 5 Karten in einer Reihe an. Es gibt \(5!\) Möglichkeiten dies zu tun.

Wir erhalten somit:

\[ \binom{13}{1} \cdot \binom{12}{1} \cdot \binom{4}{3} \cdot \binom{4}{2} \cdot 5! \]

2. Nun kann man nur noch den Wert der Karten lesen, nicht aber die Farbe. Wie viele Möglichkeiten haben sie jetzt noch ein Fullhouse zuerst zu ziehen, und dann in einer Reihe anzuordnen? - Das Angeben der Formel genügt. - 1.5 Pkt

TipLösung

Wir ziehen einen Drilling(\(\binom{13}{1}\)) und einen Zwilling(\(\binom{12}{1}\)). Die Reihenfolge ist dabei egal.

Die Farben sind jetzt egal.

Nun ordnen wir die 5 Karten in einer Reihe an, wobei wir durch die jeweils, durch die Ordnung, der nicht unterscheidbaren Karten teilen müssen. Es gibt \(\frac{5!}{3!2!}\) Möglichkeiten dies zu tun.

Wir erhalten somit:

\[ \binom{13}{1} \cdot \binom{12}{1} \cdot \frac{5!}{3!2!} \]

Betrug 3 Pkt

Sie wollen nun beim 5-Card-Draw betrügen. Dazu haben sie sich ein zweites Deck von Karten besorgt, die von den echten Karten nicht zu unterscheiden sind. Sie haben sich dann die Beiden Karten (Pik,Ass) und (Herz, Ass), noch vor dem Ziehen, heimlich auf die Hand getan. Nun haben sie 7 Karten in der Hand:

2x(Pik,Ass), 2x(Herz, Ass), 1x(Pik,König), 1x(Kreuz,Ass), 1x(Karo,Ass)

1. Wie viele Möglichkeiten haben sie diese 7 Karten in einer Reihe anzuordnen? - Das Angeben der Formel oder Anzahl genügt. - 1 Pkt

TipLösung

Wir ordnen wir die 7 Karten in einer Reihe an, wobei wir durch die jeweils, durch die Ordnung, der nicht unterscheidbaren Karten teilen müssen.

\[ \frac{7!}{2!2!} \]

2. Wie viele Möglichkeiten haben sie nur 5 dieser 7 Karten in einer Reihe anzuordnen? - Das Angeben der Formel oder Anzahl genügt. - 2 Pkt

TipLösung

Wir machen eine Fallunterscheidung

1. Die 5 Karten die wir auswählen enthalten beide ganze Tupel. \[ \binom{3}{1}\frac{5!}{2!2!} \]

2. Die 5 Karten die wir auswählen enthalten nur eines der beiden Tupeln, dafür ganze Tupel. \[ \binom{2}{1} \frac{5!}{2!} \]

3. Die 5 Karten die wir auswählen enthalten beide Tupel, aber jeweils nur halb. \[ 5! \]

4. Die 5 Karten die wir auswählen enthalten beide Tupel, aber eines nur noch nur halb und das andere ganz. \[ \binom{2}{1} \binom{3}{2} \frac{5!}{2!} \]

Setzen wir die Fälle zusamen erhalten wir:

\[ \binom{3}{2}\frac{5!}{2!2!} + \binom{2}{1}\frac{5!}{2!} + 5! + \binom{2}{1}\binom{3}{2}\frac{5!}{2!} = 5!(\frac{3}{4} + 1 + 1 + 3) = 5! \cdot (5 + \frac{3}{4}) = 690 \]

Stirling Zahlen 2 Pkt

1. 4 Spieler sitzen in einem Kreis/Zyklus. Jeder zieht 5 Karten. Dann legen alle Spieler ihre Karten so auf den Tisch, sodass die gezogenen Karten einen Zyklus bilden.

Wie viele Zyklen lassen sich so mit den 52 Karten bilden? - Das Angeben der Formel oder Anzahl genügt. - 1 Pkt

TipLösung

Wenn 4 Spieler 5 Karten ziehen un in einem Zyklus anordnen, dann bilden die 20 Karten einen Zyklus.

Wir können \(\binom{52}{20}\) karten auswählen und mit diesen dann jeweils \(\left[{ 20 \atop 1} \right] = (20-1)! = 19!\) Zyklen bilden.

Dann ist die Antwort:

\[ \binom{52}{20} \cdot 19! \]

2. Wie viele Möglichkeiten gibt es die 52 Karten auf 4 Spieler zu verteilen, wobei nicht jeder Spieler zwingend eine Karte erhalten muss? Heißt jeder Spieler \(i ∈ [4]\) hat \(k_i ∈ \{0,...,52\}\) Karten mit \[ \sum_{i \in [4]} k_i = 52 \]

Das Angeben der Formel oder Anzahl genügt. - 1 Pkt

TipLösung

Wir partionieren die Menge aller Karten auf bis zu 4 Spieler (\(\left\{52 \atop i\right\}\)). Dabei wählen wir jeweis die \(i\) vielen Spieler aus den 4 Spielern aus (\(\binom{4}{i}\)).

Dann ist die Antwort:

\[ \sum_{i = 1}^{4} \binom{4}{i} \left\{52 \atop i \right\} \]

Graphentheorie 10 Pkt

Wälder 3 Pkt

Gegeben sei der folgende Wald \(W\):

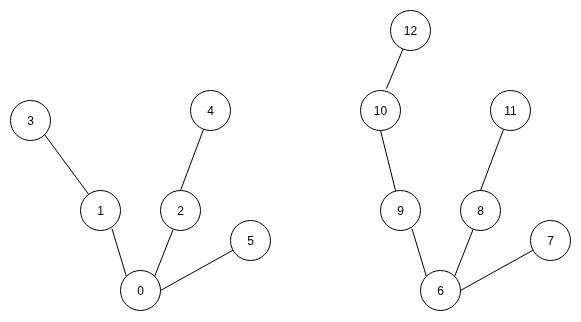
1. Was ist der Durchmesser der beiden zusammenhängenden Teilgraphen (Bäume) von \(W\)? Geben Sie dazu die jeweiligen Knotenpaare an, die dem Durchmesser entsprechen. - 1 Pkt

TipLösung

Linker Baum: - Durchmesser: 4 - Knotenpaar: (3, 4)

Rechter Baum: - Durchmesser: 5 - Knotenpaar: (12, 11)

2. Geben Sie die Prüfercodes der beiden Bäume von \(W\) an. - 1 Pkt

TipLösung

Linker Baum: \(1,0,2,0\)

Rechter Baum: \(5,8,5,9,10\)

4. Ist jeder Wald bipartit? Begründen Sie! - 1 Pkt

TipLösung

Ja, denn jeder Baum ist bipartit(Korollar 6.38). Da ein Wald aus mehren Bäumen besteht, ist auch jeder Wald bipartit.

Färbung von Graphen 2 Pkt

Ordnen Sie die untenstehenden Graphen nach ihrer chromatische Zahl \(χ\) von klein nach gross mit \(≺_χ\) dazwischen, falls die chromatische Zahl echt kleiner ist, oder mit \(≡_χ\) dazwischen falls die chromatische Zahl gleich ist.

\(K^4\), \(K_{9,3}\), \(C_7\), \(Q_8\), \(M_{7,3}\).

TipLösung

\(χ(K^4) = 4\)

\(χ(K_{9,3}) = 2\)

\(χ(C_7) = 3\)

\(χ(Q_8) = 2\)

\(χ(M_{7,3}) = 2\)

Als Reihenfolge ergibt sich: \[ K_{9,3} ≡_χ Q_8 ≡_χ M_{7,3} ≺_χ C_7 ≺_χ K^4 \]

Eigenschaften von Graphen 5 Pkt

Gegeben sei der folgende Graph \(G\):

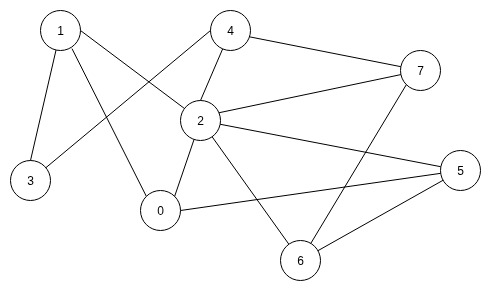
1. Welche Gradfolge besitzt der Graph \(G\)? - 1 Pkt

TipLösung

\[ (6,3,3,3,3,3,3,2) \]

2. Ist \(G\) planar? Begründen Sie ihre Antwort. - 1 Pkt

TipLösung

Ja, \(G\) ist planar, denn er enthält keinen Untergraphen der isomorph zu \(K_5\) oder \(K_{3,3}\) ist. Nach dem Theorem (6.34) von Kuratowski ist er planar.

Mit unter anderem sieht der ebene Graph so aus: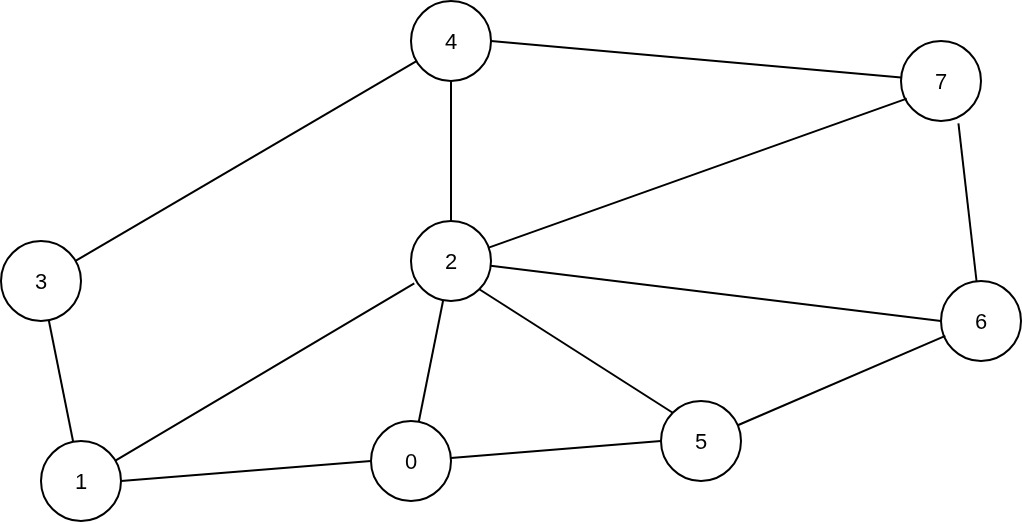

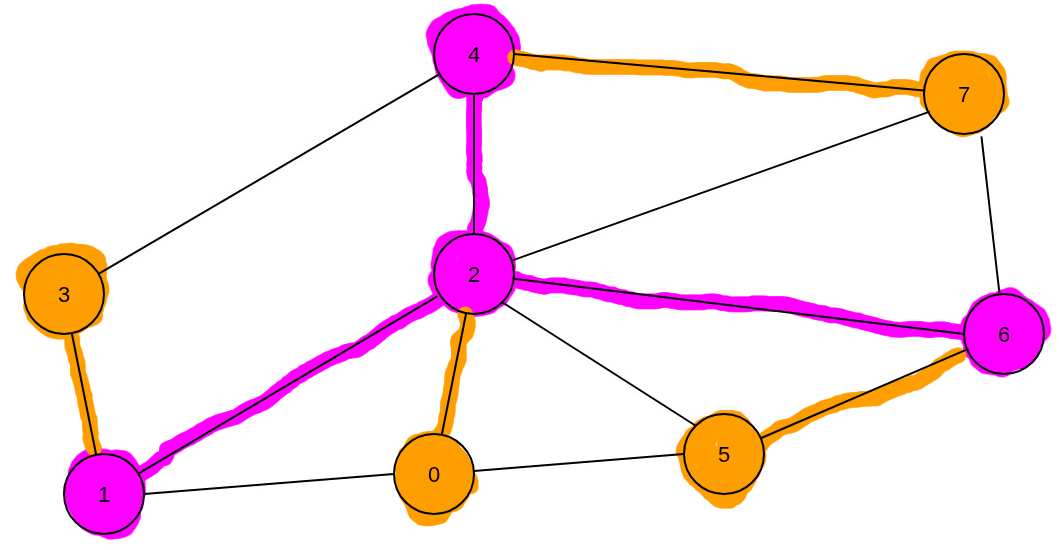
3. Ist der Baum mit dem Prüfer-Code 212624 ein Spannbaum von \(G\)? Begründen Sie ihre Antwort. - 1 Pkt

TipLösung

Ja, und zwar mit dem folgendem Spannbaum: \[ (\{0,..., 7\}, \{\{1,3\}, \{1,2\}, \{0,2\}, \{2,4\}, \{2,6\},\{4,7\},\{5,6\}\}) \]

4. Ist \(G\) bipartit? Begründen Sie ihre Antwort. - 1 Pkt

TipLösung

Nein, den entfernt man den Knoten 2 und seine Kanten, so erhät man den \(C_7\) als Teilgraphen, welcher ungerade ist. Und demnach ist nach Theorem 6.37 \(G\) nicht bipartit.

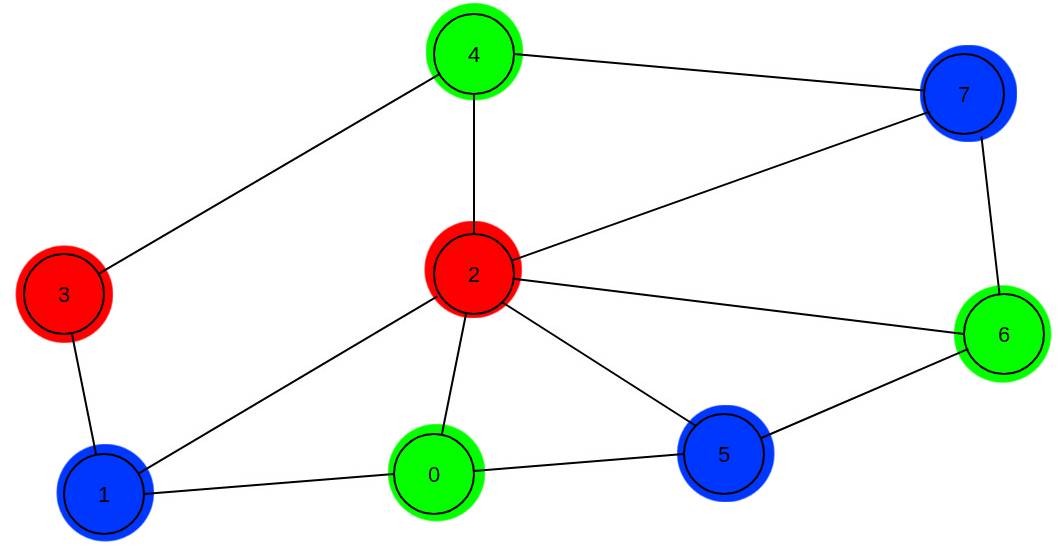
5. Was ist die chromatische Zahl \(χ(G)\) und der chromatische Index \(χ'(G)\)? - 1 Pkt

TipLösung

Da \(C_7\) ein Teilgraph von \(G\) ist, ist \(χ(G) ≥ 3\). Da \(G\) planar ist, gilt nach dem Vier-Farben-Theorem \(χ(G) ≤ 4\). Da genau ein Knoten (Knoten 3) nicht mit dem Knoten 2 verbunden ist, kann dieser Knoten die selbe Farbe wie Knoten 2 erhalten. Somit ist \(χ(G) = 3\).

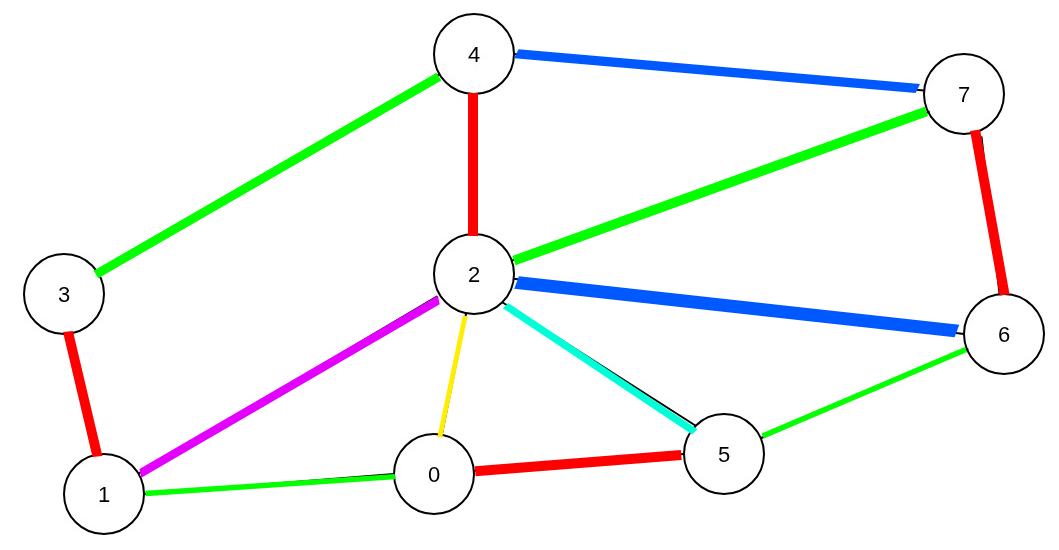
Der maximale Grad von \(G\) ist ∆(G) = 6. Nach dem Theorem von Vizing gilt somit \(6 ≤ χ'(G) ≤ 7\). Da aber der restliche Graph(\(C_7\)) gut mit 3 Farben gefärbt werden kann, ist \(χ'(G) = 6\).

Abzählen 10 Pkt

Doppeltes Abzählen 2 Pkt

Zeigen Sie, dass ein Maximum \(g:ℕ → ℕ\) bezüglich der Größe von Halbordnungen auf \([n] = \{1, ..., n\}\) existiert, sodass jede Halbordnung \(⪯ \; ⊆ [n] × [n]\) gerade nicht mehr als \(g(n)\) Elemente hat, bzw: \[ (∀⪯)\left[|⪯| ≤ g(n)\right] \quad \wedge \quad (∃⪯)\left[|⪯| = g(n)\right] \]

Berechnen Sie \(g(n)\) explizit.

TipLösung

Sei \(⪯\) eine Halbordnung auf \([n]\). Da \(⪯\) reflexiv ist, enthält \(⪯\) mindestens die \(n\) Paare \((a,a)\) für alle \(a ∈ [n]\).

Nun betrachten wir die strikte Halbordnung \(≺ \; = \; ⪯ ∖ \{(a,a) ∈ [n]\}\). Für jedes Paar \(\{a,b\}\subseteq [n]\) gibt es maximal ein element in \(≺\), entweder \((a,b)\), \((b,a)\) oder keines der beiden. Somit enthält \(≺\) höchstens \(\binom{n}{2}\) Paare.

Also ist \(g(n) = n + \binom{n}{2} = \frac{n(n+1)}{2}\).

Inklusions-Exklusionsprinzip 4 Pkt

Berechnen Sie mittels dem Inklusions-Exklusionsprinzip die Anzahl der Zahlen in \([90]\), die aus der multiplikation zweier Primzahlen bestehen. - Hinweis: Primzahlen \(≤ \sqrt{90}\) sind \(\{2,3,5,7\}\)

TipLösung

Definiere Die Menge aller vielfacher von einer Zahl a in \([90]\) als: \[ V(a) := \{ x ∈ [2,90] ∩ ℕ \mid (∃n ∈ [90])[x = a · n] \} \] Dann gilt: \(|V(a)| = \lfloor\frac{90}{a}\rfloor - 1\)

Unteranderem ist dann für \(a \ne b\)

\[ |V(a) ∩ V(b)| = \left\lfloor\frac{90}{\text{kgV}(a,b)}\right\rfloor \]

Die Betrachte die Menge A welche alle Zahlen in \([90]\) enthält die durch mindestens eine der Primzahlen \(2,3,5,7\) teilbar sind, die somit auch die Menge aller Zahlen in \([90]\) enthält die aus der multiplikation von mindestens zwei Primzahlen bestehen.

\[ A = V(2) ∪ V(3) ∪ V(5) ∪ V(7) \]

Die Menge B enthält alle Zahlen in \([90]\) die aus der multiplikation von mindestens drei Primzahlen bestehen. \[ \begin{aligned} B = V(2²) ∪ V(3²) ∪ V(5²) ∪ V(7²)\\ ∪ V(2*3) ∪ V(2*5) ∪ V(2*7)\\ ∪ V(3*5) ∪ V(3*7) ∪ V(5*7)\\ \end{aligned} \]

Bemerke: \(B ⊆ A\) also ist \(|A ∖ B| = |A| - |B|\)

Die gesuchte Menge der Zahlen die aus der multiplikation zweier Primzahlen bestehen ist \(Λ = A ∖ B\)

Wir können \(|Λ| = |A| - |B|\) mit dem Inklusions-Exklusionsprinzip berechnen.

Wir berechnen: \(|A|\)

\[ \begin{aligned} |A| = \\ \left\lfloor\frac{90}{2}\right\rfloor - 1 + \left\lfloor\frac{90}{3}\right\rfloor - 1 + \left\lfloor\frac{90}{5}\right\rfloor - 1 + \left\lfloor\frac{90}{7}\right\rfloor - 1\\ - \left\lfloor\frac{90}{2*3=6}\right\rfloor - \left\lfloor\frac{90}{2*5=10}\right\rfloor - \left\lfloor\frac{90}{2*7=14}\right\rfloor\\ - \left\lfloor\frac{90}{3*5=15}\right\rfloor - \left\lfloor\frac{90}{3*7=21}\right\rfloor - \left\lfloor\frac{90}{5*7=35}\right\rfloor\\ + \left\lfloor\frac{90}{2*3*5=30}\right\rfloor + \left\lfloor\frac{90}{2*3*7=42}\right\rfloor + \left\lfloor\frac{90}{2*5*7=70}\right\rfloor\\ = [44 + 29 + 17 + 11] - [15 + 9 + 6 + 6 + 4 + 2] + [3 + 2 + 1]\\ = 101 - 42 + 6\\ = 65 \end{aligned} \]

Wir berechnen: \(|B|\)

Therme die mehfach vorkommen wie \[ \begin{aligned} |V(2²) ∩ V(3*5)|\\ = |V(2²) ∩ V(2*5) ∩ V(3*2)| = |V(2²) ∩ V(2*5) ∩ V(3*5)| = |V(2²) ∩ V(3*5) ∩ V(3*2)|\\ = |V(2²) ∩ V(2*5) ∩ V(3*2) ∩ V(3*5)|\\ = \left\lfloor\frac{90}{2²*3*5=60}\right\rfloor \end{aligned} \]

,

\[ \begin{aligned} |V(3³) ∩ V(2²)|\\ = |V(2*3) ∩ V(3³) ∩ V(2²)|\\ = \left\lfloor\frac{90}{3²*2²}\right\rfloor \end{aligned} \]

oder

\[ \begin{aligned} |V(2*3) ∩ V(3*5)| = |V(3*5) ∩ V(2*5)| = |V(2*3) ∩ V(2*5)|\\ = |V(2*3) ∩ V(2*5) ∩ V(3*5)|\\ = \left\lfloor\frac{90}{2*3*5=30}\right\rfloor \end{aligned} \] können wir dabei teilwese weglassen solange wir sie genügend zählen.

\[ \begin{aligned} |B| = \\ \left\lfloor\frac{90}{2²=4}\right\rfloor - 1 + \left\lfloor\frac{90}{3²=9}\right\rfloor - 1 + \left\lfloor\frac{90}{5²=25}\right\rfloor - 1 + \left\lfloor\frac{90}{7²=49}\right\rfloor - 1\\ + \left\lfloor\frac{90}{2*3=6}\right\rfloor - 1 + \left\lfloor\frac{90}{2*5=10}\right\rfloor - 1 + \left\lfloor\frac{90}{2*7=14}\right\rfloor - 1\\ + \left\lfloor\frac{90}{3*5=15}\right\rfloor - 1 + \left\lfloor\frac{90}{3*7=21}\right\rfloor - 1 + \left\lfloor\frac{90}{5*7=35}\right\rfloor -1\\ - \left\lfloor\frac{90}{2²*3=12}\right\rfloor - \left\lfloor\frac{90}{2²*5=20} \right\rfloor - \left\lfloor\frac{90}{2²*7=28}\right\rfloor\\ - \left\lfloor\frac{90}{3²*2=18}\right\rfloor - \left\lfloor\frac{90}{3²*5=45}\right\rfloor - \left\lfloor\frac{90}{3²*7=63}\right\rfloor\\ - \left\lfloor\frac{90}{5²*2=50}\right\rfloor - \left\lfloor\frac{90}{5²*3=75}\right\rfloor\\ - 2\left\lfloor\frac{90}{2*3*5=30}\right\rfloor - 2\left\lfloor\frac{90}{2*3*7=42}\right\rfloor - 2\left\lfloor\frac{90}{2*5*7=70}\right\rfloor\\ + \left\lfloor\frac{90}{2²*3*5 = 60}\right\rfloor + \left\lfloor\frac{90}{2²*3*7 = 84}\right\rfloor + \left\lfloor\frac{90}{2*3²*5 = 90}\right\rfloor\\ = [22 + 10 + 3 + 1 + 15 + 9 + 6 + 6 + 4 + 2] - 10\\ - [7+4+3+5+2+1+1+1+ 2*3 +2*2 + 2*1]\\ + 3\\ = 78 - 10 - 36 + 3\\ = 35 \end{aligned} \]

Also ist die Lösung: \(|Λ| = |A| - |B| = 65 - 35 = \underline{\underline{30}}\)

Schubfachschluss 4 Pkt

In einer Menge von \(n\) natürlichen Zahlen gibt es immer zwei Zahlen, deren Differenz durch \(n-1\) teilbar ist. Beweisen Sie dies mit dem Schubfachschluss. - Hinweis: Betrachten Sie die Menge “Reste der Division durch \(n-1\)”.

TipLösung

Wir betrachten die Reste der Division durch \(n-1\). Diese sind \(0, 1, 2, ..., n-2\), also insgesamt \(n-1\) verschiedene Reste.

Bemerke: zwei Zahlen \(a,b\) haben den selben Rest bei der Division durch \(n-1\) genau dann, wenn ihre Differenz durch \(n-1\) teilbar ist.

Da bei \(n\) Zahlen aber nur \(n-1\) verschiedene Reste existieren, müssen nach dem Schubfachprinzip mindestens zwei Zahlen den selben Rest haben.

Somit gibt es immer zwei Zahlen, deren Differenz durch \(n-1\) teilbar ist.